Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas.

Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:

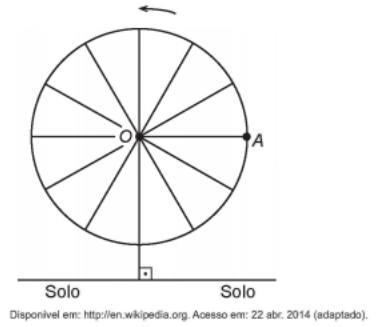
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t. Após duas voltas completas, f tem o seguinte gráfico:

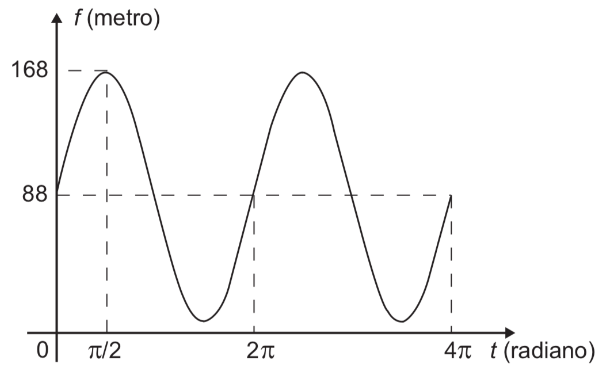
A expressão da função altura é dada por

A) f(t) = 80sen(t) + 88

B) f(t) = 80cos(t) + 88

C) f(t) = 88cos(t) + 168

D) f(t) = 168sen(t) + 88cos(t)

E) f(t) = 88sen(t) + 168cos(t)

Solução

Temos f(0) = 88, f(π/2) = 168 e f(π) = 88 quando vamos substituir os valores nas alternativas:

A) f(t) = 80.sen(t) + 88

f(0) = 80.sen(0) + 88

f(0) = 88

V

f(π/2) = 80.sen(π/2) + 88

f(π/2) = 80.1 + 88

f(π/2) = 268

V

f(π) = 80.sen(π) + 88

f(π) = 88

V

B) f(t) = 80cos(t) + 88

f(0) = 80.cos(0) + 88

f(0) = 80 + 88

f(0) = 168

X

C) f(t) = 88cos(t) + 168

f(0) = 88.cos(0) + 168

f(0) = 88.1 + 168

f(0) = 256

X

D) f(t) = 168sen(t) + 88cos(t)

f(0) = 168sen(0) + 88cos(0)

f(0) = 0 + 88

V

f(π/2) = 168.sen(π/2) + 88.cos(π/2)

f(π/2) = 168.1 + 88.0

f(π/2) = 168

V

f(π) = 168.sen(π) + 88.cos(π)

f(π) = 168.0 + 88.(-1)

f(π) = -88

X

E) f(t) = 88sen(t) + 168cos(t)

f(0) = 88.sen(0) + 168.cos(0)

f(0) = 0 + 168

X

A alternativa que se encaixa em todos os pontos é a

Alternativa A