Um engenheiro projetou um automóvel cujos vidros das portas dianteiras foram desenhados de forma que suas bordas superiores

Um engenheiro projetou um automóvel cujos vidros das portas dianteiras foram desenhados de forma que suas bordas superiores fossem representadas pela curva de equação y = log (x), conforme a figura.

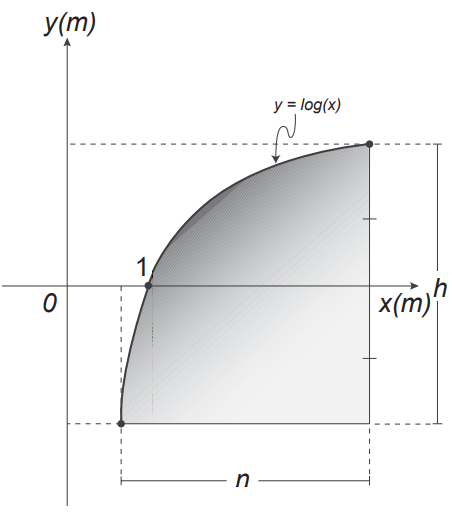
A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do vidro e a base do vidro seja paralela ao eixo x. Obedecendo a essas condições, o engenheiro determinou uma expressão que fornece a altura h do vidro em função da medida n de sua base, em metros.

A expressão algébrica que determina a altura do vidro é

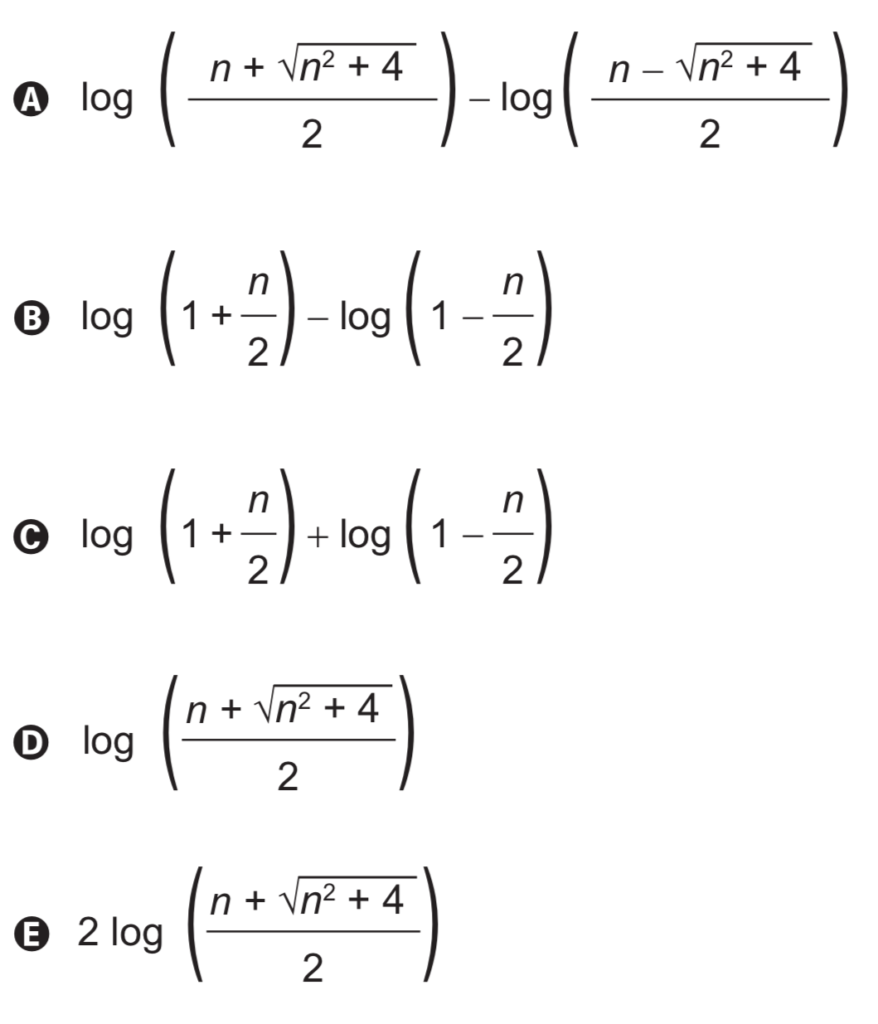
Solução

Sabemos que o eixo x divide h ao meio, ou seja, em cima de x temos h/2 e abaixo temos h/2.

Podemos observar os dois pontos destacados de coordenadas A:(x₁,-h/2) e B:(x₂,h/2), precisamos descobrir quanto vale as coordenadas x de cada ponto.

Sabemos que a diferença das coordenadas x é n, podemos observar que

x₂ =x₁ + n

Então podemos escrever as coordenadas dos pontos como A:(x₁,-h/2) e B:(x₁ + n, h/2)

Sendo y = log(x), podemos substituir as coordenadas na equação formando um sistema de duas equações

(1) -h/2 = log(x₁)

E

(2) h/2 = log(x₁ + n)

Substituindo (2) em (1) temos

– log(x₁ + n) = log(x₁)

=> log(x₁ + n)^-1 = log(x₁)

Usando as propriedades de log temos que

(x₁ + n)^-1 = x₁

=> 1/(x₁ + n) = x₁

1 = x₁² + n.x₁

x₁² + n.x₁ – 1 = 0

Por bhaskara e lembrando que x₁ é positivo, temos apenas uma raiz

x₁ = [-n + √(n² + 4)]/2

Substituindo esse valor na equação (2):

h/2 = log{[-n + √(n² + 4)]/2 + n}

h =2. log{[-n + √(n² + 4)]/2 + n}

Resolvendo a parte interna do log temos

[-n + √(n² + 4)]/2 + n = [n + √(n² + 4)]/2, então

h = [n + √(n² + 4)]/2

Alternativa E